Archimede di Siracusa

Gli studiosi sono uomini privilegiati; pochi

di loro conoscono il Greco, e la maggior

parte di loro non sa nient’altro.

Quando Newton disse:” Se ho visto più di altri, è perché stavo sulle spalle dei giganti ", uno dei giganti che doveva avere in mente era Archimede di Siracusa, il più brillante matematico, fisico e ingegnere dell’antichità. Poco si sa della sua vita. Nacque intorno al 287 a.C a Siracusa, figlio dell’astronomo Fidia, e a quanto pare trascorse gran parte della sua vita a Siracusa. Studiò presso l’Università di Alessandria sia sotto gli immediati successori di Euclide, sia sotto Euclide stesso. Era un amico e parente di Gerone II, re di Siracusa, per il quale progettò le macchine da guerra utilizzate contro gli aggressori romani, e la cui corona fu coinvolta nella scoperta della legge della spinta verso l’alto che porta il suo nome. Gerone (correttamente) sospettò che la sua corona non fosse d’oro puro e chiese ad Archimede di indagare senza danneggiarla. Si sa che Archimede meditò sul problema mentre si faceva un bagno e trovò la risposta, non appena osservò il livello dell’acqua alzarsi sino a sommergere il suo corpo. Gridando:”EUREKA! Ho trovato!”, dice questa leggenda, corse nudo per le strade di Siracusa per dire a Gerone della sua scoperta. Il suo libro sui corpi galleggianti va ben oltre la legge di Archimede e comprende complicati problemi di stabilità. Allo stesso modo Sull’Equilibrio dei Piani va oltre il principio della leva e risolve complicati problemi come trovare il baricentro di un segmento parabolico. In queste, come in altre sue opere, Archimede utilizza l’approccio euclideo: da un insieme di semplici postulati, deduce le sue affermazioni con logica impeccabile. Come primo scrittore che costantemente legò matematica e fisica, Archimede è diventato il padre della fisica come scienza. La fisica di Aristotele fu pubblicata un secolo prima, ma è solo una lunga sfilza di speculazioni infondate, totalmente prive di qualsiasi relazione quantitativa. Archimede è stato anche il primo ingegnere scientifico, l’uomo alla ricerca di principi generali che applicò a specifici problemi d’ingegneria. La sua applicazione del principio della leva per le macchine da guerra in difesa di Siracusa sono ben noti, inoltre applicò ancora lo stesso principio per trovare il volume del segmento di una sfera con un metodo di bilanciamento insolitamente bello di cui avremo più da dire più avanti in questo capitolo. Ha usato lo stesso metodo per determinare i volumi di altri solidi di rotazione (ellissoide, paraboloide, iperboloide) e per trovare il centro di gravità del semicerchio e dell’emisfera. Non è noto quante opere di Archimede siano andate perdute (una delle più importanti, Il Metodo, è venuta alla luce solo nel 1906), ma i suoi libri rimasti, tra cui Sulle Spirali, Sulla Misurazione del Cerchio, La Quadratura della Parabola, Sui Conoidi e Sferoidi, Sulla Sfera e il Cilindro, Il Libro dei Lemmi e altri, sono ineguagliate da qualsiasi altro prodotto dell’antichità.

 

Non solo a causa dei risultati meravigliosi contenuti in questi libri, ma anche perché Archimede fu un pioniere del Metodo. Partendo dal concetto di “uguale” arrivò a quello di “arbitrariamente vicino a” o “tanto vicino quanto desiderato” (che Euclide aveva enunciato ma non attivamente usato) e quindi raggiunse la soglia del calcolo differenziale , proprio come il suo metodo di quadratura della parabola raggiunse la soglia del calcolo integrale (alcuni ritengono che la abbia superata).

E’ stato anche il primo a ideare un metodo per calcolare π con un qualunque grado desiderato di precisione. Esso si basa sul fatto che il perimetro di un poligono regolare di n lati inscritto in una circonferenza è minore della circonferenza, mentre il perimetro di un poligono simile circoscritto alla circonferenza è maggiore della circonferenza (vedi figura sotto). Rendendo n sufficientemente grande, i due

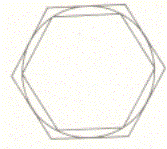
Il metodo di Archimede per calcolare p

 

perimetri si avvicineranno alla circonferenza arbitrariamente, uno per difetto, l’altro per eccesso. Archimede iniziò con un esagono, e progressivamente raddoppiando il numero dei lati, arrivò a un poligono di 96 lati, il che diede:

 

                                  (1)

o in notazione decimale:

(2)

 

Ciò che Archimede ha fatto senza trigonometria, e senza notazione decimale (o altra notazione posizionale) è un’illustrazione della sua tenacia (vedi la traduzione di Heath “Sulla Misura del Cerchio” proposizione 3 e seguenti). Tuttavia potremmo utilizzarle entrambe per procedere con i calcoli. Se   è metà dell’angolo sotteso da un lato di un poligono regolare di n lati nel centro della circonferenza, allora la lunghezza del lato inscritto è

   (3)

e quella del lato circoscritto è

   (4)

 

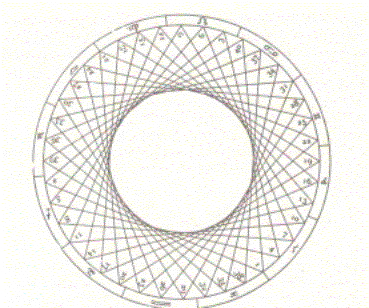
Un poligono regolare di 40 lati. Non è stata disegnata la circonferenza interna.

 

Per quanto riguarda la circonferenza C del cerchio abbiamo quindi:

o dividendo per 2r,

. (5)

 

Se il numero iniziale di n lati è raddoppiato k volte, questo produce

 

 

Rendendo k sufficientemente grande, i limiti inferiori e superiori si avvicineranno a p arbitrariamente. Archimede non utilizzò, ovviamente, funzioni trigonometriche; comunque per n = 6 ottenne ,  con il teorema di Pitagora; e le funzioni rimanenti nella (6) , possono essere ottenute con l’uso successivo delle formule di dimezzamento (la qual cosa corrisponde a trovare proporzioni in triangoli rettangoli). Per k = 4, i due poligoni avranno 96 lati, e questo porterà ai limiti della (1), se le radici quadrate coinvolte nelle formule di dimezzamento sono approssimate da numeri razionali leggermente minori per il limite inferiore, e da numeri razionali leggermente maggiori per il limite superiore. Questo è descritto ancora più facilmente nella terminologia moderna che realmente fatto senza trigonometria o un sistema decimale per l’aritmetica di accompagnamento. Le formule di dimezzamento più somiglianti alla procedura di Archimede sono

 

 

 

che gli hanno permesso (in effetti) di trovare  e  da  e . Per l’esagono, Archimede ha approssimato  col valore leggermente inferiore di 265/153; un poligono a 12 lati lo impegnò nel rapporto  , che ha semplificato a , e il poligono finale di 96 lati coinvolge una radice quadrata di un numero che nel sistema decimale ha dieci cifre!

Come sia riuscito ad estrarre le sue radici quadrate con tale accuratezza, sempre avendo cura di rispettare così sottilmente il lato piccolo o il lato grande, come richiesto dai limiti, è uno degli enigmi che questo straordinario uomo ci ha lasciato. Ma sembra che Archimede sia andato anche oltre. Erone di Alessandria, nella sua Metrica (circa il 60 A.C., ma non scoperta fino al 1896), si riferisce a un lavoro di Archimede che da allora è andato perso, in cui Archimede dà i limiti:

 

o

 

dove il limite superiore u, nella copia del lavoro di Erone trovata a Costantinopoli nel 1896, è dato da:

 

Tuttavia, questo è evidentemente un errore che si deve essere insinuato durante la trascrizione della copia, perchè è molto più scadente rispetto al limite superiore 3+1/7 trovato da Archimede in precedenza. Erone aggiunge:” poiché questi numeri sono scomodi per le misurazioni, p viene ridotto al rapporto di numeri più piccoli, ossia 22/7.

I limiti ottenuti da Archimede ne La Misura del Cerchio erano

o in notazione decimale

 

Archimede ha anche mostrato che una curva scoperta da Conone di Alessandria poteva, come la quadratrice di Ippia, essere utilizzata per rettificare (e quindi quadrare) il cerchio. La curva è oggi chiamata la spirale di Archimede; è definita come il luogo geometrico piano di un punto che si sposta di moto rettilineo uniforme lungo un raggio mentre il raggio ruota di moto circolare uniforme attorno alla sua estremità. È questa la curva tracciata da una puntina che striscia radialmente verso

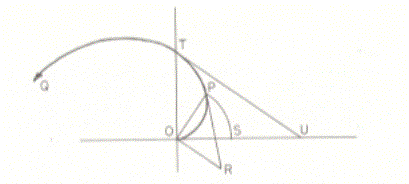
Rettificazione della circonferenza per mezzo della Spirale di Archimede

 

l’esterno su un disco fonografico rotante. Sia P un punto della spirale (vedi figura sopra), e la tangente in P intersechi la perpendicolare alla retta OP in R. Archimede mostrò nel suo libro “Sulle Spirali” che il segmento OR (cioè la sottotangente polare nel punto P) è uguale alla lunghezza dell’arco circolare PS di raggio OP, dove S è l’intersezione con il raggio iniziale OU.

Ne consegue che OU equivale a ¼ della circonferenza di un cerchio con raggio OT, cosicché

 (8)

e l’area del triangolo OTU è

 

da cui

l’area del cerchio con raggio OT = 4 volte l’area del triangolo OTU

e il cerchio è quadrato di nuovo, anche se non è di gradimento della geometria greca; le obiezioni sono le stesse come nel caso della quadratrice di Ippia.

Archimede ha usato una doppia reductio ad absurdum per provare che il segmento OR e l’arco PS erano uguali in lunghezza. Noi lo dimostreremo più rapidamente con la geometria differenziale. Sia OP = r e l’angolo SOP = q. Quindi dalla definizione della Spirale di Archimede,

 (9)

 

dove k è la costante uguale al rapporto delle velocità angolari e lineari. Come è indicato nei libri di testo di geometria differenziale, la lunghezza della sottotangente in coordinate polari è:

 (10)

e poiché , abbiamo da (9), (10), e dalla figura

 

 (11)

 

come volevasi dimostrare. In particolare per ,

 

 (12)

Tali furono alcuni dei contributi del più grande genio dell’antichità alla storia del pi greco e della quadratura del cerchio. Anche se gli investigatori successivamente hanno trovato approssimazioni numeriche migliori, il metodo poligonale di Archimede è rimasto insuperato fino a quando diciannove secoli più tardi furono trovati in Inghilterra un prodotto infinito e una frazione continua infinita poco prima che la scoperta del calcolo differenziale portasse a un approccio totalmente nuovo al problema.

In fisica, nessuno è giunto vicino alla statura di Archimede per più di 18 secoli, fino a quando Galileo Galilei osò sfidare le menzogne di Aristotele. Le ombre di quelle menzogne sono con noi persino adesso. C’è la storia della matematica che non scusa Archimede per essersi sporcato le mani con il lavoro sperimentale. Nel tardo 1968, ci viene detto che “egli mise poco valore nei suoi congegni meccanici”, e che ”considerava i suoi congegni e invenzioni come sordidamente commerciali” (1965). Commenti simili si trovano in quasi tutti i libri sull’argomento, sostenendo l’osservazione di Philip Guedella “La storia si ripete; gli storici si ripetono l’un l’altro”. Il mito ripetitivo è stato iniziato da Plutarco, che nel primo secolo d.C. ha scritto che

 

Considerando la meccanica e ogni arte utilitaristica come ignobile e volgare, egli dette la sua zelante

devozione solo a quei soggetti la eleganza e sottigliezza sono non impastoiate dalle necessità della vita.

 

Ora Plutarco non poteva forse sapere cosa Archimede avesse considerato ignobile e volgare; il suo credo era buono come il vostro o il mio. Ma proprio come per diciannove secoli, gli storici hanno riecheggiato Plutarco, così Plutarco fa eco all’atteggiamento di Platone e Aristotele, i padri dello snobismo intellettuale. Essi hanno insegnato che la sperimentazione era adatta solo per gli schiavi, e che le leggi della natura potevano essere dedotte soltanto dall’uomo di alto intelletto; e Aristotele ha usato il suo nobile intelletto per scoprire che i corpi più pesanti cadono a terra più velocemente; che gli uomini hanno più denti rispetto alla donna; che la Terra è al centro dell’universo; che i corpi celesti non cambiano mai; e molto di più di tale saggezza, perché era uno scrittore molto prolifico. Di fatto Aristotele è stato sconfitto sul proprio terreno, per mezzo della pura deduzione intellettuale dell’osservazione sperimentale. Molto tempo prima che Galileo Galilei facesse cadere delle palle di legno e di piombo dalla Torre pendente di Pisa, egli pose la seguente domanda:” Se una pietra di 10 libbre cade 10 volte più velocemente di una da 1 libbra, cosa succede se lego insieme le due pietre? La combinazione cadrà più velocemente della pietra di 10 libbre perché pesa 11 libbre, o cadrà più lentamente perché la pietra da 1 libbra ritarderà la pietra da 10 libbre?”

Il commento di Plutarco sull’atteggiamento di Archimede per l’ingegneria è una elaborazione con nessun fondamento diverso dallo snobismo aristotelico. Il libro di

 

 

La legge della leva W₁r₁=W₂r₂, dove W₁ e W₂ sono pesi (o altre forze)

 

 

 

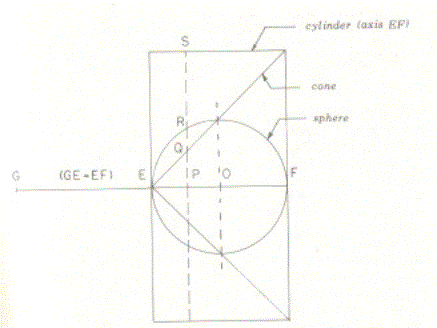
Il principio della leva applicato alla geometria. Un piano PS, perpendicolare a GF in un generico punto P taglierà la sfera, il cono e il cilindro secondo cerchi con raggi PR, PQ e PS, rispettivamente. Archimede dimostrò che i primi due cerchi (i cui pesi sono proporzionali alle loro aree) posti sulla leva GEF con fulcro E bilanciano esattamente il terzo cerchio in P.

Da questo derivò il volume di un segmento sferico e dell’intera sfera ( ).

 

Archimede “Il Metodo” è stato scoperto solo nel secolo presente, e getta qualche luce interessante sul punto. La reductio ad absurdum è al giorno d’oggi un metodo popolare di dimostrazione; esso, tuttavia, ha l’inconveniente che si deve conoscere il risultato in anticipo per conoscere l’alternativa che deve essere confutata. Come questo risultato sia stato originariamente derivato non trapela dalla prova. Dal momento che Archimede usava molto spesso reductiones ad absurdum, gli storici spesso si sono meravigliati che con quel metodo egli abbia originariamente scoperto i suoi meravigliosi risultati.

Risulta in molti casi che fece questo con un metodo di analogia o di modellazione (come è chiamata oggi), basato sui principi di niente altro che le ignobili, volgari e commercialmente sordide invenzioni che ha addotto di avere inventato con tale riluttanza. Nel Metodo, lui scrive a Eratostene, il Bibliotecario ad Alessandria che noi abbiamo già incontrato (pag 46):

 

Archimede saluta Eratostene

Ti ho spedito nella precedente occasione alcuni dei teoremi scoperti da me, semplicemente scrivendoti gli enunciati e invitandoti a scoprire le dimostrazioni, che a quel tempo non ti diedi.

Poi le dimostrazioni di questi teoremi le ho scritte in questo libro e ora te lo invio. Inoltre vedendo in te, come già dissi, uno studente volenteroso,[…] ho ritenuto opportuno scriverti e spiegare in dettaglio nello stesso libro la particolarità di un certo metodo, con cui sarà possibile per te indagare alcuni dei problemi di matematica mediante la meccanica. Questa procedura è, sono convinto, non meno utile persino delle stesse dimostrazioni dei teoremi; perché certe cose prima mi sono diventate chiare con un metodo meccanico, malgrado dovessero essere dimostrate dopo tramite la geometria perché la loro indagine col sopraccitato metodo non forniva una vera dimostrazione. Ma quando abbiamo acquisito, col metodo, alcune conoscenze dei problemi, è la strada più facile per fornire la dimostrazione anzicché trovarla senza alcuna conoscenza precedente.

 

Un chiaro esempio di questo metodo è l’applicazione di Archimede del principio della leva per ricavare il volume di un segmento sferico oltre che dell’intera sfera, come indicato nella figura di pag. 71. Così grande valore dette Archimede a questa scoperta, che chiese che una sfera inscritta in un cilindro fosse incisa sulla sua lapide, e questo è stato fatto perché, anche se la lapide è andata perduta, abbiamo una descrizione della tomba da parte di Cicerone, che la visitò nel I secolo a.C. durante il suo incarico di questore in Sicilia.

Non è senza interesse ricordare come è stato recuperato Il Metodo. Fu trovato nel 1906 a Costantinopoli su un palinsesto, che è, una pergamena il cui testo originale è stato lavato (per recuperare la pergamena) e sostituito con un testo diverso. Se l’originale è stato lavato via non perfettamente, esso può essere ripristinato con una speciale fotografia. In questo caso il testo originale era una copia del X secolo di alcune opere note di Archimede, ma pure includente l’unico testo superstite de Il Metodo. Gli zeloti medievali non sempre, come il vescovo dello Yucatan o i Crociati a Costantinopoli, bruciavano i libri scientifici come opera del diavolo. A volte essi pulivano il testo per la pergamena, in modo che da poterla sporcare con la loro immondizia superstiziosa.